Tiling Paterns

Truchet Tiling

In information visualization and graphic design, Truchet tiles are square tiles decorated with patterns that are not rotationally symmetric. When placed in a square tiling of the plane, they can form varied patterns, and the orientation of each tile can be used to visualize information associated with the tile’s position within the tiling.

The tile originally studied by Truchet is split along the diagonal into two triangles of contrasting colors. The tile has four possible orientations.

A second common form of the Truchet tiles, due to Smith (1987), decorates each tile with two quarter-circles connecting the midpoints of adjacent sides. Each such tile has two possible orientations.

Implementation

Base Tile

from pynodes import *
from pynodes.math import *

@tree
def create_tile():
    """Tile"""

    curve = CurveCircle(resolution=3)

    curve[0].set_position((0, 0, 0))

    curve[1].set_position((1, 0, 0))

    curve[2].set_position((0, 1, 0))

    curve.transform((-0.5, -0.5, 0))

    arc = CurveArc(radius=0.5, sweep_angle=pi * 0.51).transform((-0.5, -0.5, 0))

    arc2 = arc.Curve.transform(rotation=(0, 0, pi))

    with frame("Select Tile to Output"):

        tile = curve.fill_curve()

        tile = arc.join(arc2)

    return tile

Truchet Tiling

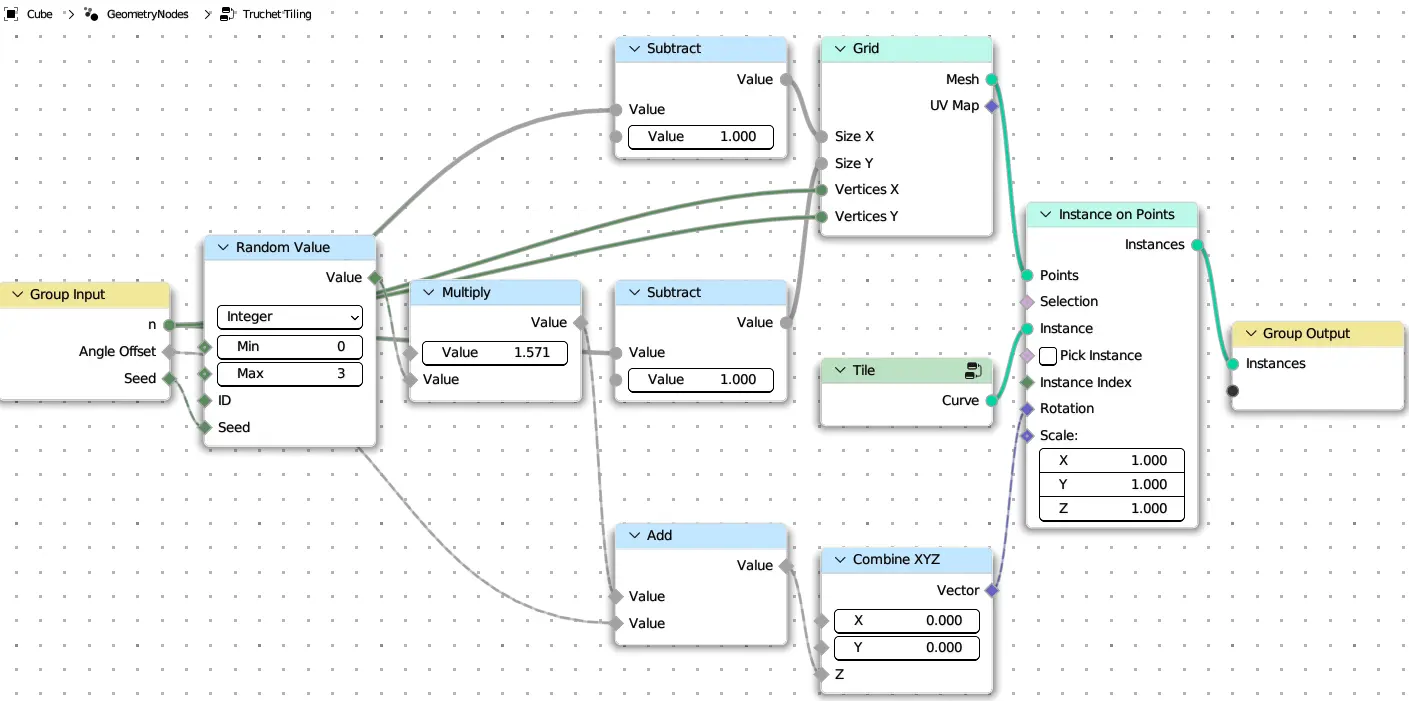
@tree
def truchet_tiling(n: Integer = 20, angle_offset: Float = (0, 0, pi / 2), seed: Integer = 0):

    tile = create_tile()

    grid = MeshGrid(n - 1, n - 1, n, n).mesh

    angle = pi / 2 * RandomInteger(0, 3, seed=seed)

    tiles = tile.on_points(grid, rotation=(0, 0, angle + angle_offset))

    return tiles