Fractals Geometry

Sierpinski Triangle 3D

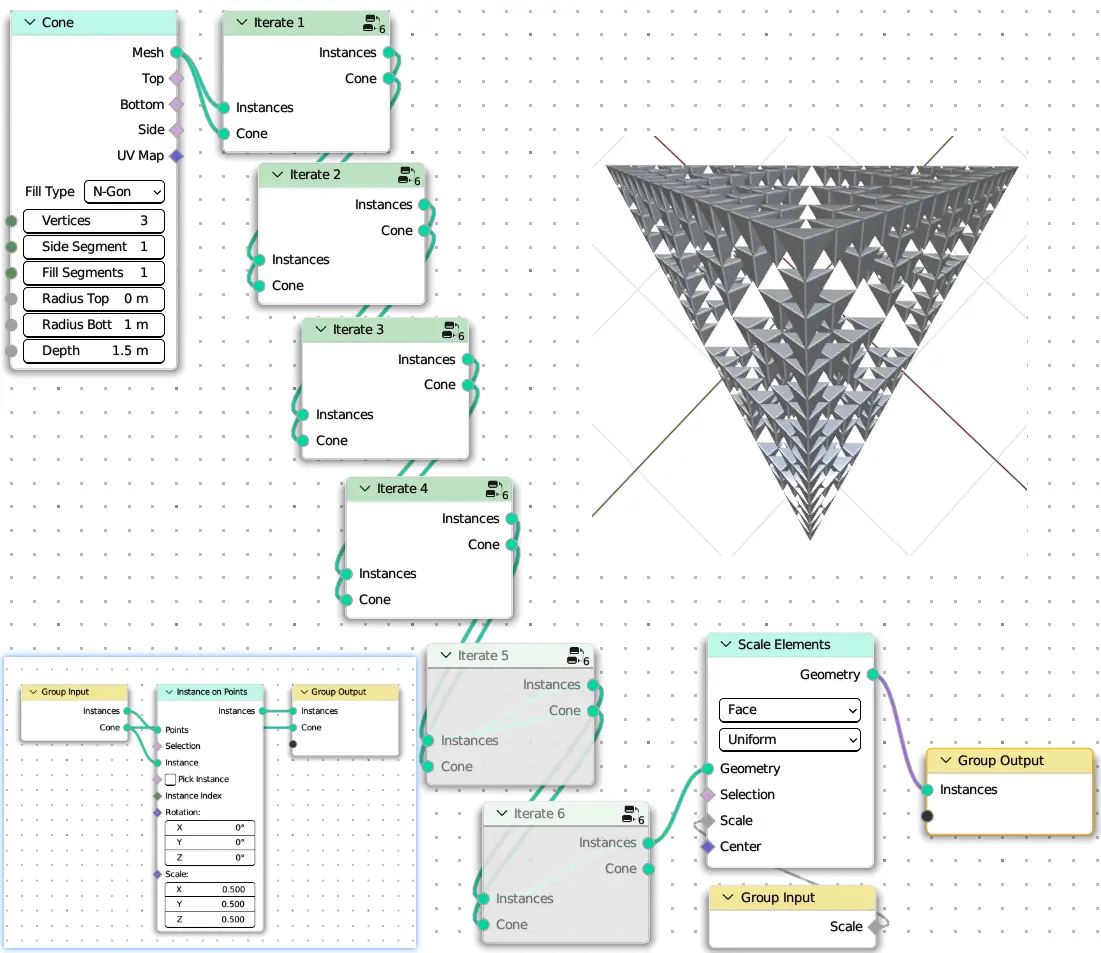
Sierpinski Triangle

@tree
def iterate_sierpinski(instances: Instances, cone: Mesh):
    """Iterate Sierp."""
    instances = cone.Instances.on_points(instances, scale=0.5)
    return instances, cone

@tree
def sierpinski_fractal(scale: Float = (2, 0.1, 10)):
    cone = MeshCone(vertices=3, depth=1.5).mesh
    instances, cone = iterate_sierpinski(cone, cone)
    instances.node.label = f"Iterate 1"

    for i in range(5):
        instances, cone = iterate_sierpinski(instances, cone)
        instances.node.label = f"Iterate {i+2}"

    return instances.scale_elements(scale=scale)

Menger Sponge

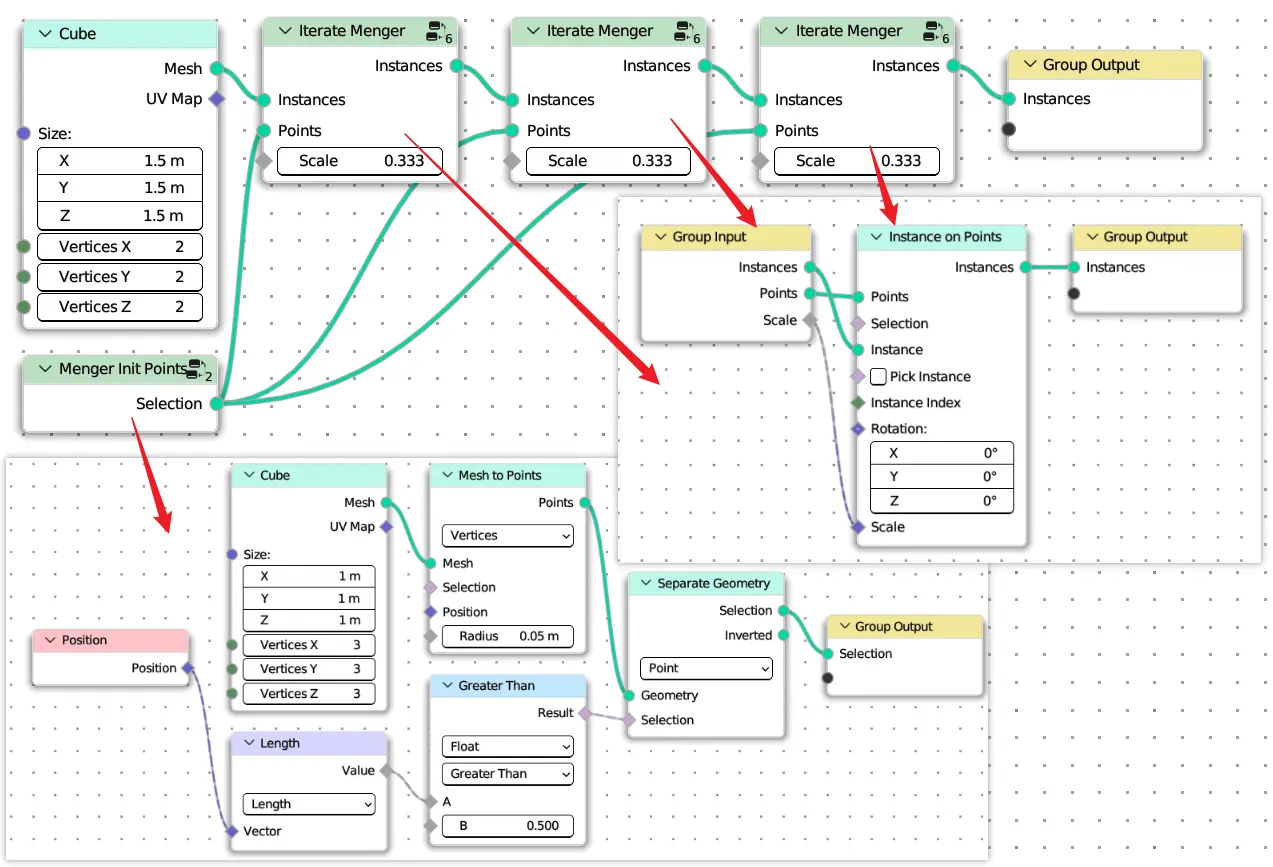
Menger Sponge

@tree
def iterate_menger(instances: Instances, points: Points, scale: Float = (1 / 3, 0, 1 / 3)):
    return instances.on_points(points, scale=scale)

@tree
def menger_init_points():
    points = MeshCube(1, 3, 3, 3).mesh.to_points()
    return points[points.position.length > 0.5].select()

@tree
def menger_sponge():
    cube = MeshCube(1.5).mesh
    points = menger_init_points()
    instances = iterate_menger(cube, points)

    for i in range(2):
        instances = iterate_menger(points=points, instances=instances)

    return instances

Pythagoras Tree

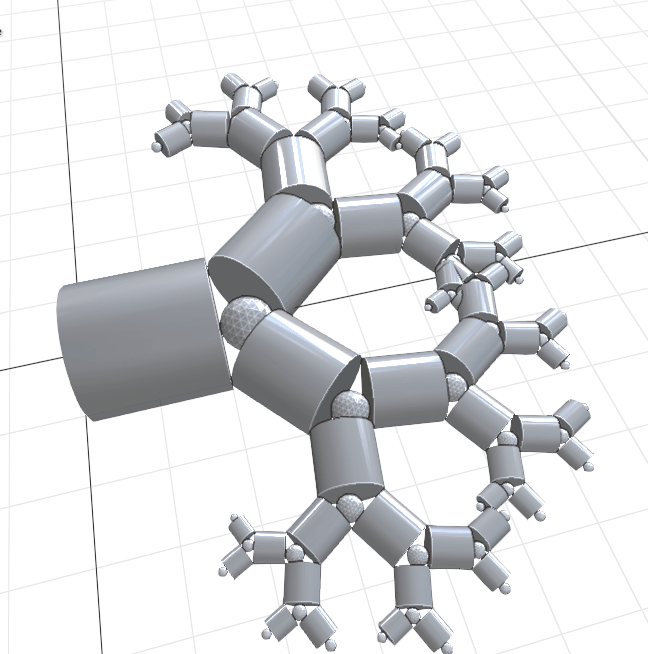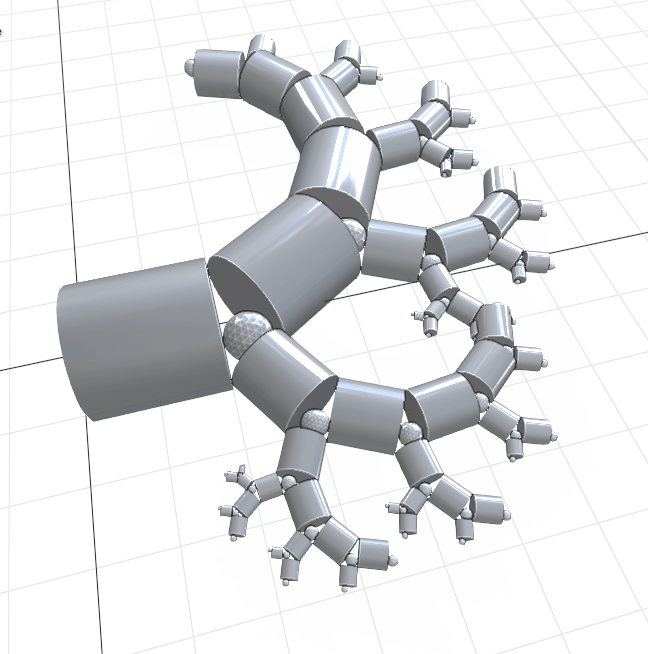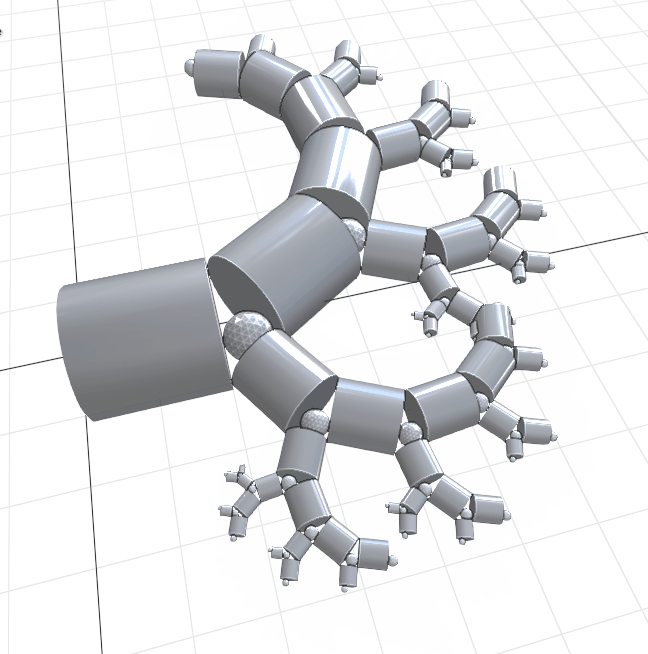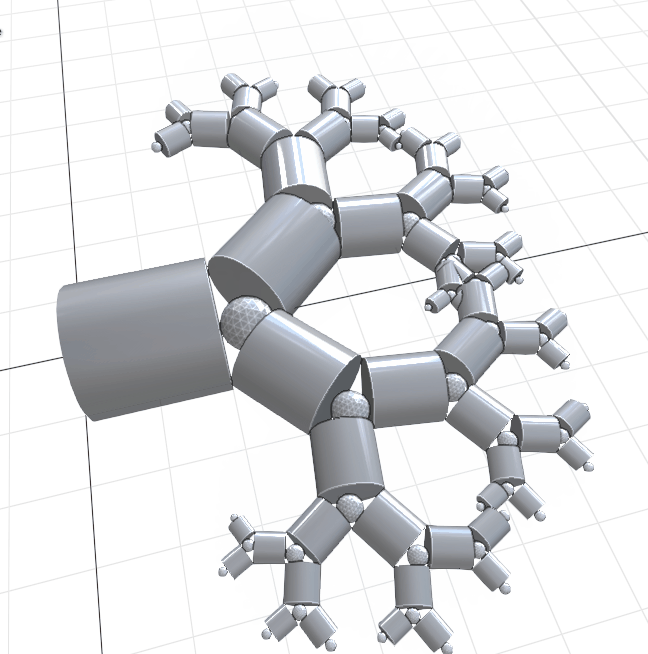
pythagoras_tree

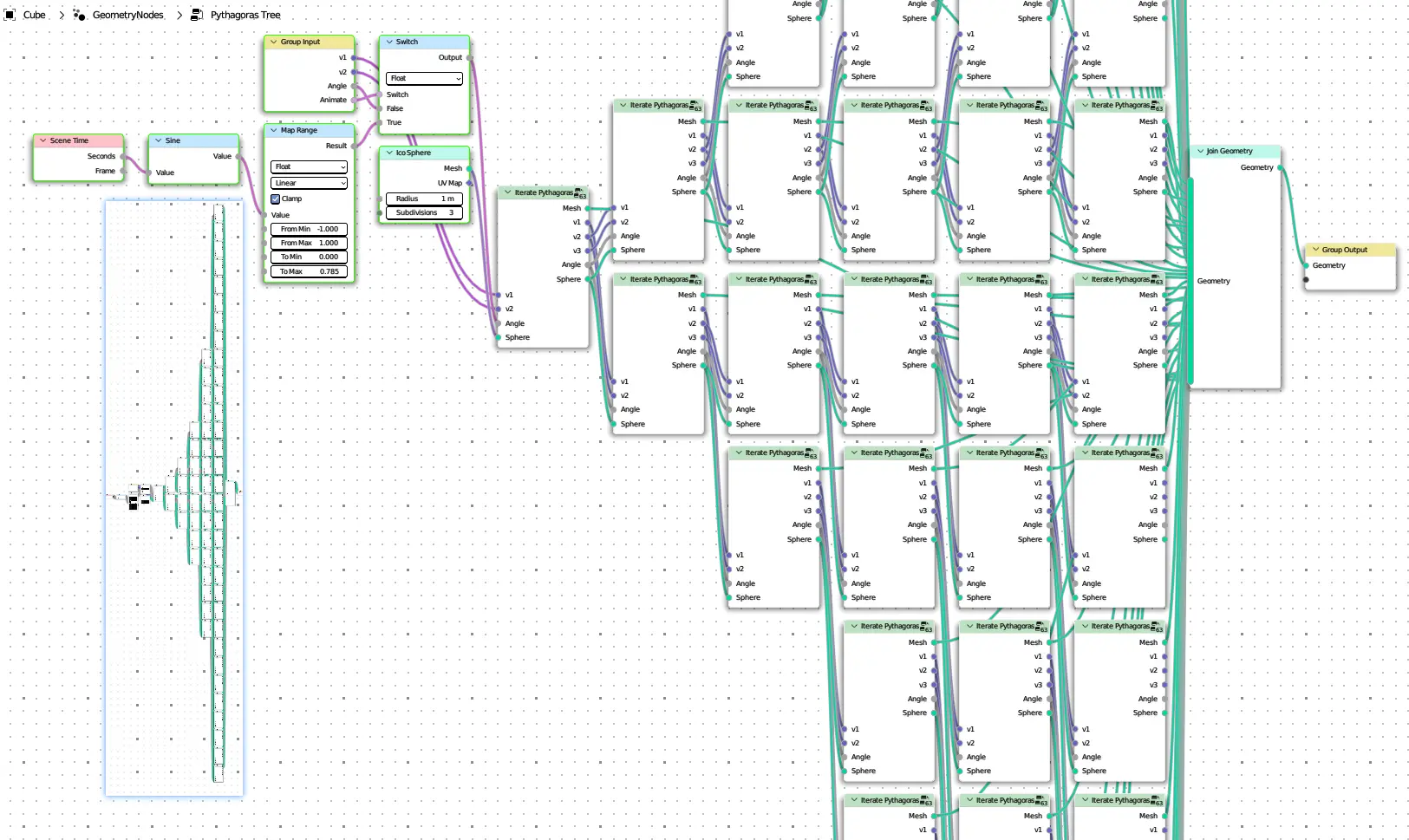
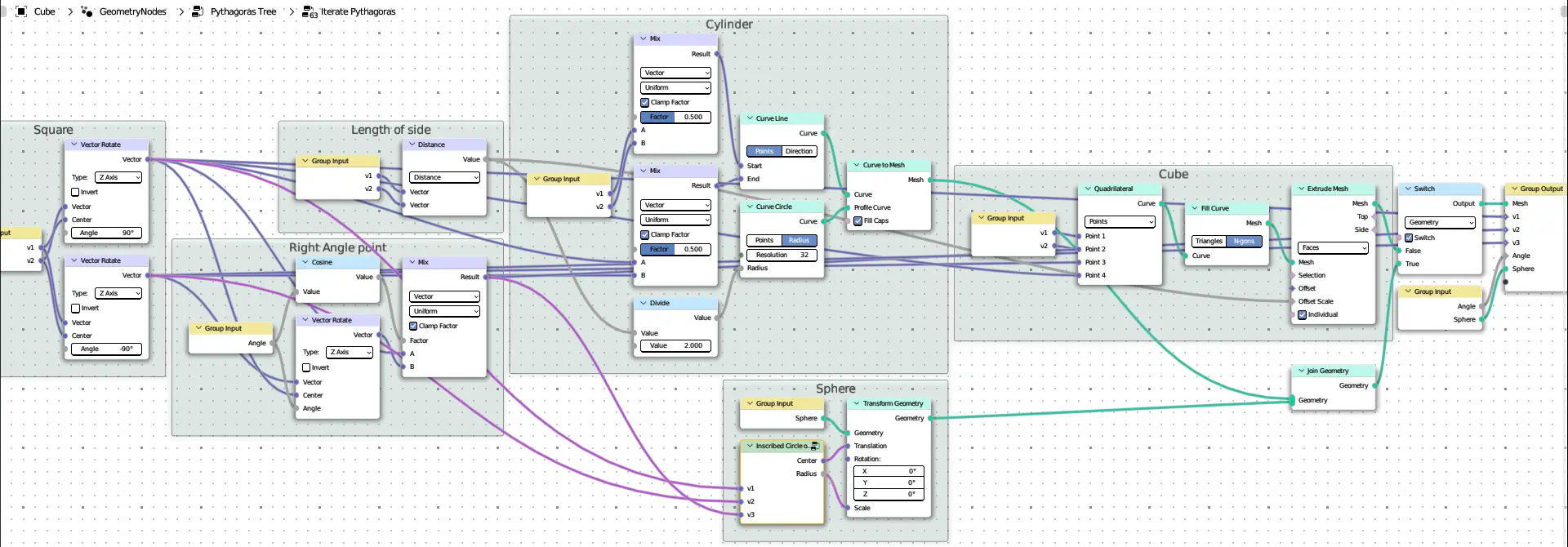
from pynodes import *
from pynodes.math import *

# Calculate the center and radius of the tangent circle of a right triangle. v3 is the right Angle point
@tree
def inscribed_circle(v1: Vector, v2: Vector, v3: Vector):
    """Inscribed Circle of Right Triangle"""

    with frame("Length of side"):
        c = v1.distance(v2)
        a = v2.distance(v3)
        b = v3.distance(v1)

    with frame("Perimeter"):
        l = c + a + b

    with frame("Radius: a + b = c + 2r"):
        r = (a + b - c) / 2

    with frame("Center of circle"):
        x = (a * v1.x + b * v2.x + c * v3.x) / l
        y = (a * v1.y + b * v2.y + c * v3.y) / l

    return CombineXYZ(x, y)("Center"), r("Radius") # Rename the ouput socket
    # return CombineXYZ(x, y), r # this is also OK


@tree
def iterate_pythagoras(v1: Vector, v2: Vector, angle: Float = (pi / 6, 0, pi / 2), sphere: Mesh = None):

    with frame("Length of side"):
        length = v1.distance(v2)

    with frame("Square"):
        v3 = v2.rotate("Z_AXIS", center=v1, angle=pi / 2)
        v4 = v1.rotate("Z_AXIS", center=v2, angle=-pi / 2)

    with frame("Right Angle point"):
        v5 = v4.rotate("Z_AXIS", center=v3, angle=angle)
        v5 = v3.mix(v5, cos(angle))

    with frame("Cube"):
        rect = Quadrangle(v1, v2, v4, v3)
        cube = rect.filled_ngons.extrude(length).mesh

    with frame("Cylinder"):
        line = v1.mix(v2).line_to(v3.mix(v4))
        cylinder = line.to_mesh(CurveCircle(length / 2), True)

    with frame("Sphere"):
        center, radius = inscribed_circle(v3, v4, v5)
        # sphere = MeshIcoSphere(radius, 1).mesh.transform(center)
        sphere_transformed = sphere.Mesh.transform(center, scale=radius)

    mesh = cube.switch(True, cylinder.join(sphere_transformed))

    return mesh("Mesh"), v3('v1'), v5('v2'), v4('v3'), angle("Angle"), sphere


def iterate_n(v1, v2, angle, sphere, curves: list, n=3):
    if n == 0:
        return
    mesh, v1, v2, v3, angle, sphere = iterate_pythagoras(v1, v2, angle, sphere)
    curves.append(mesh)
    iterate_n(v1, v2, angle, sphere, curves, n - 1)
    iterate_n(v2, v3, angle, sphere, curves, n - 1)


@tree
def pythagoras_tree(
    v1: Vector = (-1, 0, 0),
    v2: Vector = (1, 0, 0),
    angle: Float = (pi / 6, 0, pi / 2),
    animate: Boolean = True,
):
    curves = []

    sphere = MeshIcoSphere(subdivisions=3).mesh

    iterate_n(v1, v2, angle.switch(animate, sin(SceneTime().seconds).map_range(-1, 1, 0, pi / 4)), sphere, curves, 6)

    return join(*curves)

Quadratic Koch 3D

quadratic_koch_3d

from pynodes import *


@tree
def iterate(points: Points, instance: Instances):

    normal = points.capture_vector_on_faces(points.normal)

    points = points.Mesh.to_points("FACES")

    return instance.on_points(points, rotation=normal.align_euler_to_vector("Z"), scale=1 / 3)


@tree
def quadratic_koch_3d():

    mesh = MeshGrid(3, 3, 4, 4).mesh

    base_mesh = mesh[4].extrude_faces().mesh

    iterated_mesh = iterate(base_mesh, base_mesh)
    iterated_mesh.node.label = "Iterate 1"

    iterated_mesh = iterate(iterated_mesh, base_mesh)
    iterated_mesh.node.label = "Iterate 2"

    iterated_mesh = iterate(iterated_mesh, base_mesh)
    iterated_mesh.node.label = "Iterate 3"

    return iterated_mesh