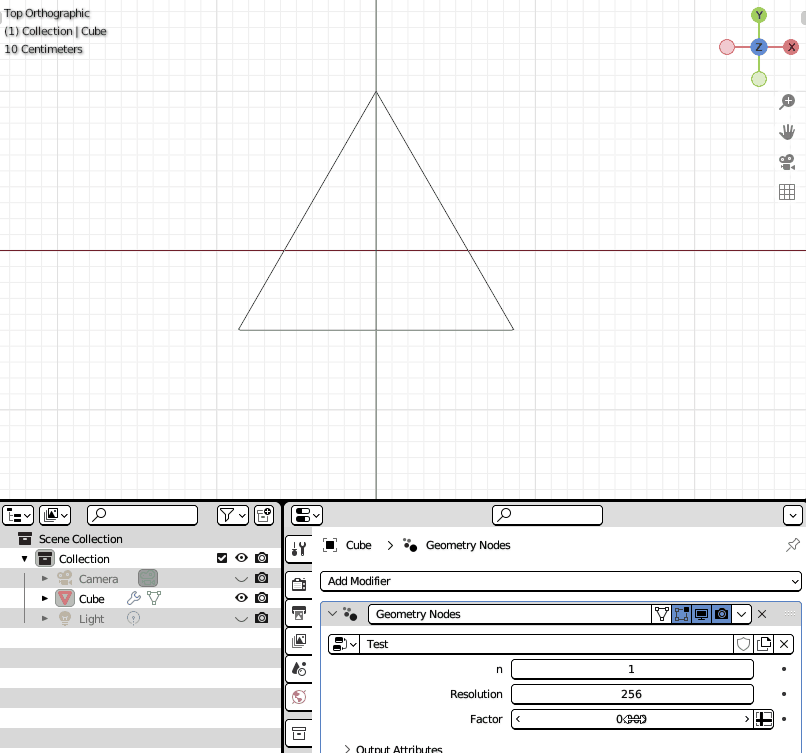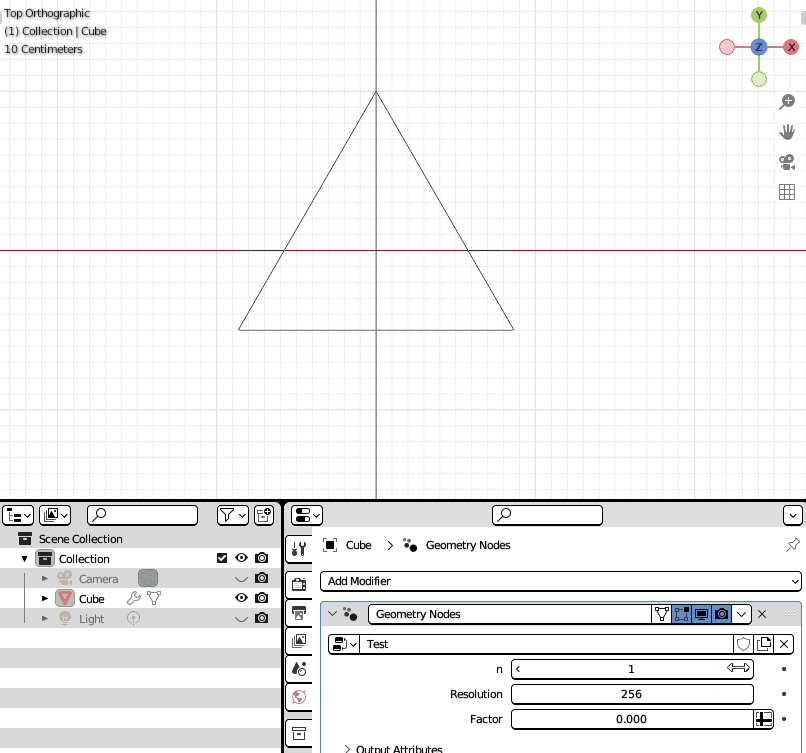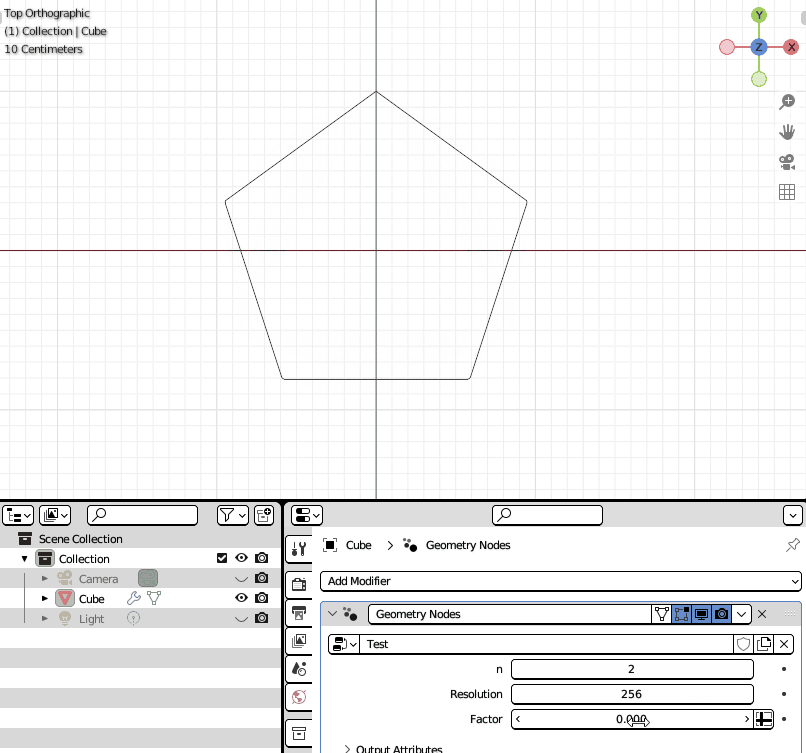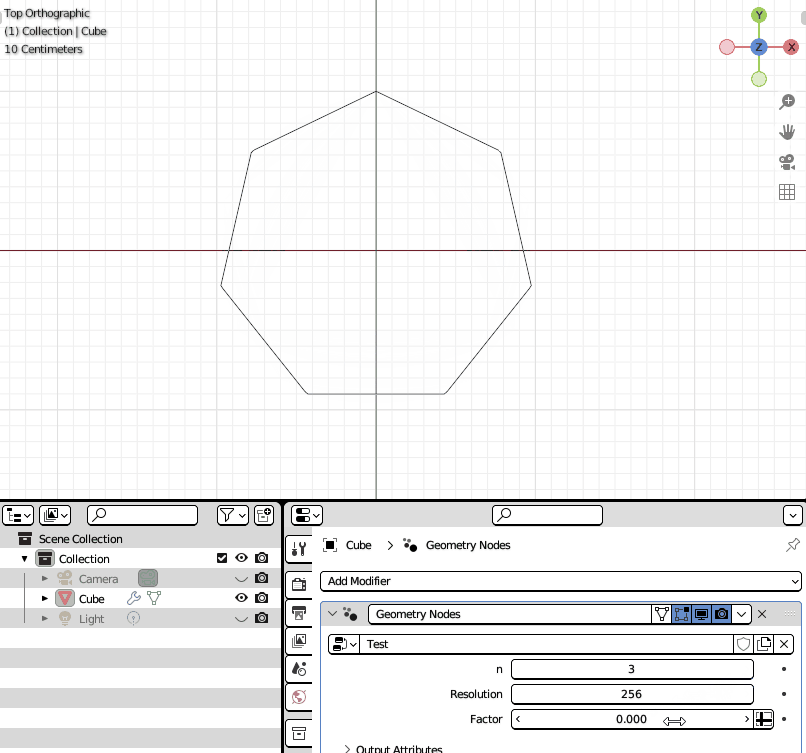
Reuleaux Polygon

In geometry, a Reuleaux polygon is a curve of constant width made up of circular arcs of constant radius.

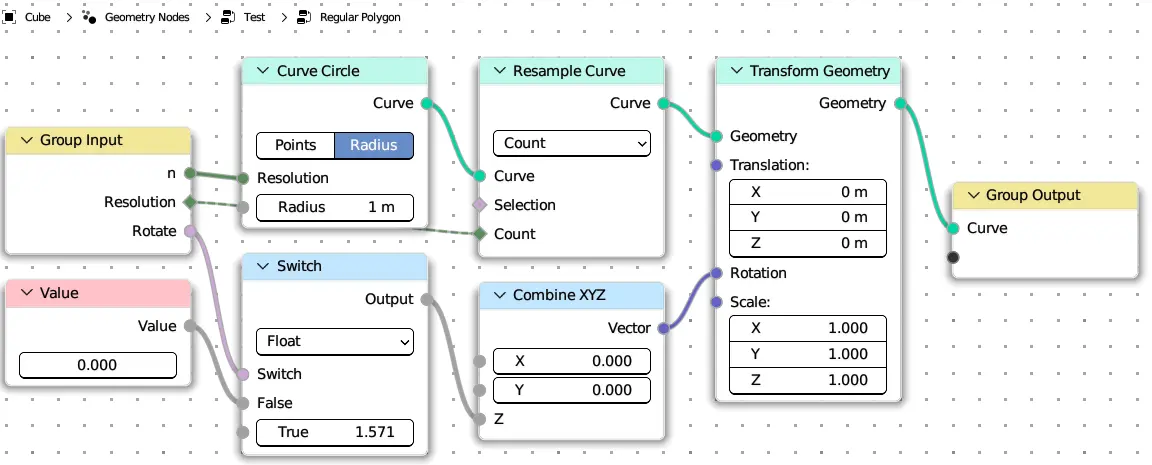
Regular Polygon

regular_polygon

from pynodes import *
from pynodes.math import *

@tree
def regular_polygon(n: Integer = (3, 3, 10), resolution: Integer = 256, rotate: Boolean = True):

    ngon = CurveCircle(1, n).resample(resolution).transform(rotation=(0, 0, InputFloat(0).switch(rotate, pi / 2)))

    return ngon

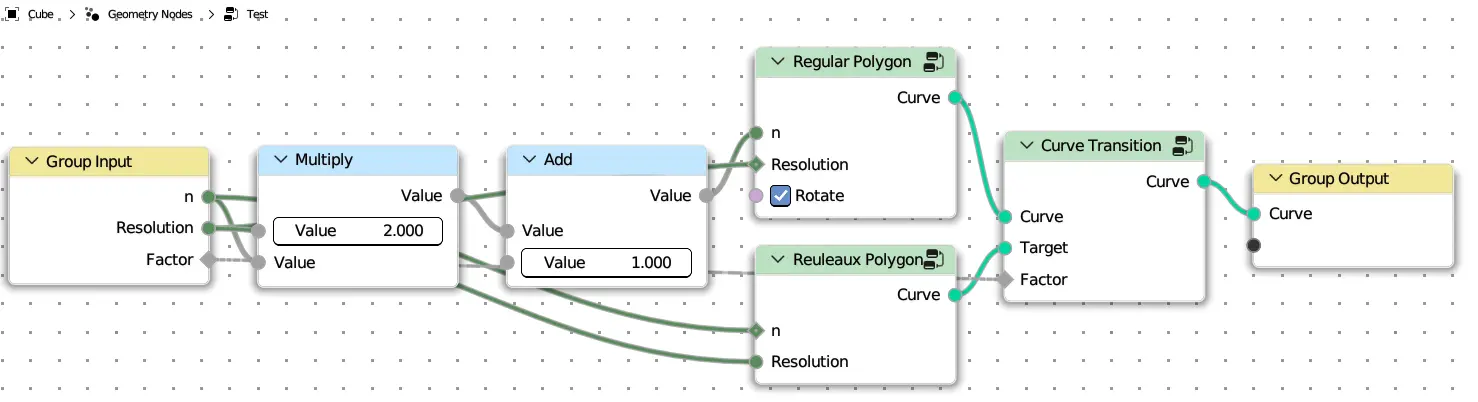
Calculate the coordinate of Reuleaux Polygon

reuleaux_coord

@tree
def reuleaux_coord(n: Integer, t: Float):

    with frame("Sector Angle"):
        k = tau / n

    with frame("Radius"):
        v = k * (n + 1) / 2
        x0, y0 = 0, 1
        x1, y1 = sin(v), cos(v)
        r = sqrt((x1 - x0) * (x1 - x0) + (y1 - y0) * (y1 - y0))

    with frame("Arc origin"):
        a = floor(t / k) * k + v
        m = sin(a)
        n = cos(a)

    with frame("Angle transform"):
        b = (floor(t / k) + 0.5) * k
        c = b + (t - b) * 0.5

    with frame("Position"):
        x = m + r * sin(c)
        y = n + r * cos(c)

    return CombineXYZ(x, y, 0)

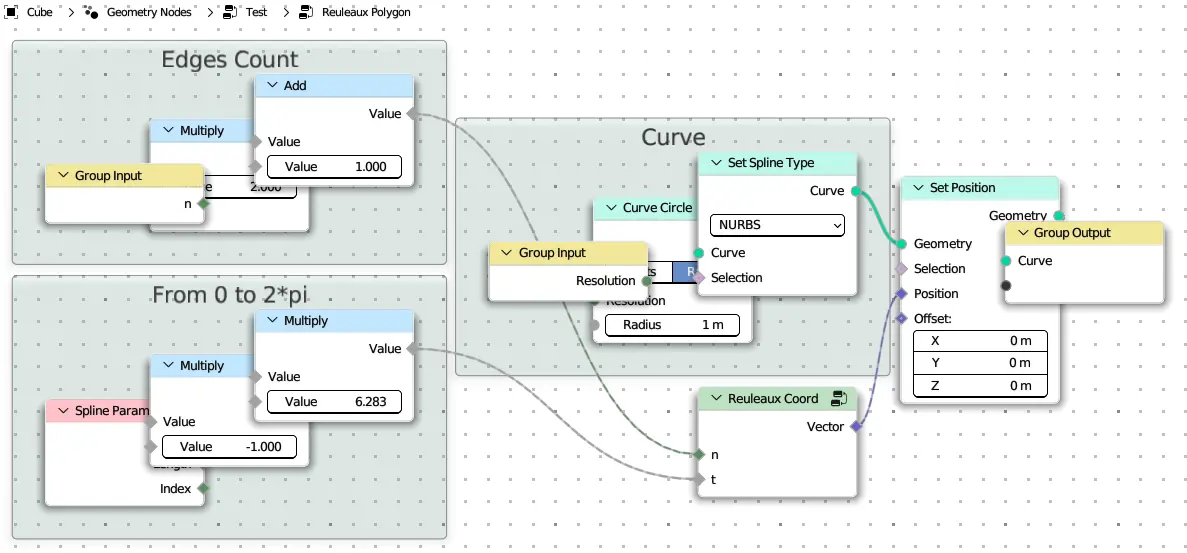
N-side Reuleaux Polygon

reuleaux_polygon

@tree
def reuleaux_polygon(n: Integer = (1, 1, 5), resolution: Integer = 256):

    with frame("Curve"):

        curve = CurveCircle(resolution=resolution).set_spline_type_nurbs()

    with frame("From 0 to 2*pi"):
        t = -curve.parameter.factor * tau

    with frame("Edges Count"):
        n = 2 * n + 1

    curve.set_position(reuleaux_coord(n, t))

    return curve

Curve Transition

curve_transition

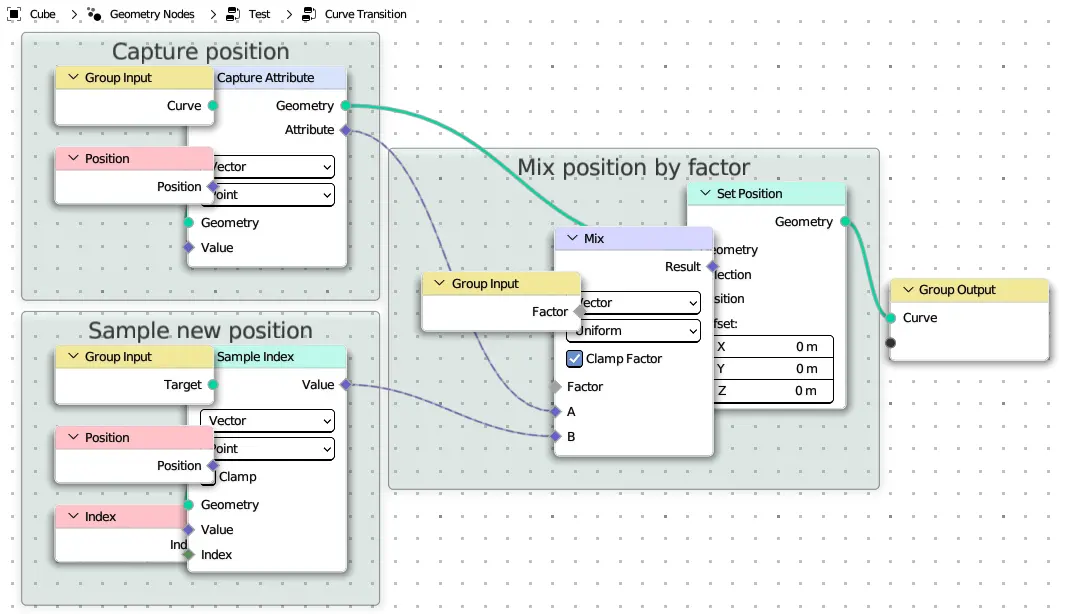
@tree
def curve_transition(curve: Curve, target: Curve, factor: Float = (0, 0, 1)):

    with frame("Capture position"):

        pos = curve.capture_vector_on_points(curve.position)

    with frame("Sample new position"):

        new_pos = target.sample_vector_at_index(target.position, target.index)

    with frame("Mix position by factor"):

        curve.set_position(pos.mix(new_pos, factor))

    return curve

Result Test

test

@tree
def test(n: Integer = (1, 1, 10), resolution: Integer = (256, 0), factor: Float = (0, 0, 1)):

    curve1 = regular_polygon(2 * n + 1, resolution)

    curve2 = reuleaux_polygon(n, resolution)

    return curve_transition(curve1, curve2, factor)